最近复习了一些基础知识,摘取了一些重要的做了一点推导,也为了之后可能面试会用到。应该是机器学习类的,但是也懒得分那么多类了,就先放在慢学NLP下面吧。这里选择把逻辑回归和softmax归到一起来讲,原因在于更好的比较两者的异同和联系。总结为以下两点:
逻辑回归的优化目标是极大化对数似然估计,采用梯度上升来学习及更新参数 $\theta$ 向量的值。
Softmax的优化目标是极小化交叉熵损失函数,采用梯度下降和链式法则来更新各层权值。
Logistics Regression
先从线性回归开始
$$h _ { w } \left( x ^ { i } \right) = w _ { 0 } + w _ { 1 } x _ { 1 } + w x _ { 2 } + \ldots + w _ { n } x _ { n }$$
$$h _ { w } \left( x ^ { j } \right) = w ^ { T } x _ { i } = W ^ { T } X$$
$$X = \left[ \begin{array} { c } { 1 } \newline { x _ { 1 } } \newline { \dots } \newline { x _ { n } } \end{array} \right] \quad W = \left[ \begin{array} { c } { w _ { 0 } } \newline { w _ { 1 } } \newline { \dots } \newline { w _ { n } } \end{array} \right]$$
针对线性分类器而言,他解决的是回归问题,为了能更好进行分类问题的探讨,这里就引出了 Logistics 回归。
基础知识
逻辑回归是假设数据服从 Bernoulli 分布(抛硬币),因此LR属于参数模型。
其中是对于线性模型,加上了一个 Sigmoid 函数,这个也是神经网络的激活函数,拥有很多良好的特性。1. 拥有很好的激活特性,2. 求导很容易,这一点在 GD 上太重要了,对于 NN 的 BPTT 也起到了极为重要的作用。
LR 目标函数定义:$h _ { \theta } ( x ) = g \left( \theta ^ { T } x \right)$
其中 Sigmoid 函数 g(z) 的定义:$g ( z ) = \frac { 1 } { 1 + e ^ { - z } }$
Sigmoid 函数求导 $g ^ {'} (z)$ 为:
$$
\begin{aligned} g ^ { \prime } ( z ) & = \frac { d } { d z } \frac { 1 } { 1 + e ^ { - z } } \newline & = \frac { 1 } { \left( 1 + e ^ { - z } \right) ^ { 2 } } \left( e ^ { - z } \right) \newline & = \frac { 1 } { \left( 1 + e ^ { - z } \right) ^ { 2 } } \cdot \left( 1 - \frac { 1 } { \left( 1 + e ^ { - z } \right) } \right) \newline & = g ( z ) ( 1 - g ( z ) ) \end{aligned}
$$
似然函数
假设有n个独立的训练样本 { (x1, y1), (x2, y2), … , (xn, yn)},y={0, 1}。那每一个观察到的样本 (xi, yi) 出现的概率是:
$$
P \left( \mathrm { y } _ { i } , \mathrm { x } _ { i } \right) = P \left( \mathrm { y } _ { i } = 1 | \mathrm { x } _ { i } \right) ^ { y _ { i } } \left( 1 - P \left( \mathrm { y } _ { i } = 1 | \mathrm { x } _ { i } \right) \right) ^ { \mathrm { 1 } - y _ { j } }
$$
推广到所有样本下,得到整体的似然函数表达,需要将所有的样本似然函数全部相乘。这里的参数 $\theta$ 是我们要估计的参数,似然函数正比于我们的概率函数 $L ( \theta | x ) \propto P ( \operatorname { x | \theta )}$,累成后得到整体的似然函数表达:
$$
L ( \theta ) = \prod P \left( \mathrm { y } _ { i } = 1 | \mathrm { x } _ { i } \right) ^ { y _ { i } } \left( 1 - P \left( \mathrm { y } _ { i } = 1 | \mathrm { x } _ { i } \right) \right) ^ { 1 - y _ { i } }
$$
具体为
$$
\begin{aligned} L ( \theta ) & = p ( \vec { y } | X ; \theta ) \newline & = \prod _ { i = 1 } ^ { m } p \left( y ^ { ( i ) } | x ^ { ( i ) } ; \theta \right) \newline & = \prod _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { y ^ { ( i ) } } \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { 1 - y ^ { ( i ) } } \end{aligned}
$$
累乘的形式不利于进行优化分析,这里将似然函数取对数,得到对数似然函数,作为我们的最终优化目标,运用极大似然估计来求得最优的 $\theta$
$$
\begin{aligned} \ell ( \theta ) & = \log L ( \theta ) \newline & = \sum _ { i = 1 } ^ { m } y ^ { ( i ) } \log h \left( x ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h \left( x ^ { ( i ) } \right) \right) \end{aligned}
$$
最优化求解推导
利用链式法对目标函数则进行求导以求得最优参数。
$$
\frac { \partial } { \theta _ { j } } J ( \theta ) = \frac { \partial J ( \theta ) } { \partial g \left( \theta ^ { T } x \right) } * \frac { \partial g \left( \theta ^ { T } x \right) } { \partial \theta ^ { T } x } * \frac { \partial \theta ^ { T } x } { \partial \theta _ { j } }
$$
分三部分求导:
第一部分
$$
\frac { \partial J ( \theta ) } { \partial g \left( \theta ^ { T } x \right) } = y * \frac { 1 } { g \left( \theta ^ { T } x \right) } + ( y - 1 ) * \frac { 1 } { 1 - g \left( \theta ^ { T _ { x } } x \right) }
$$
第二部分
$$
\frac { \partial g \left( \theta ^ { T } x \right) } { \partial \theta ^ { T } x } = g \left( \theta ^ { T } x \right) \left( 1 - g \left( \theta ^ { T } x \right) \right)
$$
第三部分
$$
\frac { \partial \theta ^ { T } x } { \theta _ { j } } = \frac { \partial J \left( \theta _ { 1 } x _ { 1 } + \theta _ { 2 } x _ { 2 } + \cdots \theta _ { n } x _ { n } \right) } { \partial \theta _ { j } } = x _ { j }
$$
整理得到最终形式:
$$
\begin{aligned} \frac { \partial } { \partial \theta _ { j } } \ell ( \theta ) & = \left( y \frac { 1 } { g \left( \theta ^ { T } x \right) } - ( 1 - y ) \frac { 1 } { 1 - g \left( \theta ^ { T } x \right) } \right) \frac { \partial } { \partial \theta _ { j } } g \left( \theta ^ { T } x \right) \newline & = \left( y \frac { 1 } { g \left( \theta ^ { T } x \right) } - ( 1 - y ) \frac { 1 } { 1 - g \left( \theta ^ { T } x \right) } \right) g \left( \theta ^ { T } x \right) \left( 1 - g \left( \theta ^ { T } x ) \right) \right) \frac { \partial } { \partial \theta _ { j } } \theta ^ { T } x \newline & = \left( y \left( 1 - g \left( \theta ^ { T } x \right) \right) - ( 1 - y ) g \left( \theta ^ { T } x \right) \right) x _ { j } \newline & = \left( y - h _ { \theta } ( x ) \right) x _ { j } \end{aligned}
$$
因此总的 $\theta$ 更新公式为:
$$
\theta _ { j } : = \theta _ { j } + \alpha \left( y ^ { ( i ) } - h _ { \theta } \left( x ^ { ( i ) } \right) \right) x _ { j } ^ { ( i ) }
$$
速记: 对 $\theta$ 的梯度更新为输入 $x_i$ * (y真实值 - logistics 的预测计算值)
整个迭代过程就是最为一般的梯度下降,逻辑回归的似然函数是典型的凸函数,运用凸优化的方式可以保证求得最优解。要考LR的话就可以这么写了吧。
扩展
(1)正则化
上述是最基础的逻辑回归的推导形式,但是在实际中,还是要针对模型进行一些正则化,防止参数规模过大产生过拟合的情况,违背了奥卡姆剃刀。这里列出了含正则化表达式的逻辑回归目标函数:
$$
J ( \theta ) = - \frac { 1 } { N } \sum y \log g \left( \theta ^ { T } x \right) + ( 1 - y ) \log \left( 1 - g \left( \theta ^ { T } x \right) \right) + \lambda | w | _ { p }
$$
(2)关于优化方法,上述给出的是最为一般的梯度下降法,其他的凸优化方法还包括有:
- 牛顿法
- 拟牛顿法
- DFP算法
- BGFS拟牛顿法
(详见李航《统计学习方法》附录B)
(3)LR 和 SVM 的异同点
相同点:
- LR和SVM都是分类算法。
- 如果不考虑核函数,LR和SVM都是线性分类算法,也就是说他们的分类决策面都是线性的。
- LR和SVM都是监督学习算法,为判别模型。
不同点:
- 本质上是其loss function不同。
逻辑回归方法基于概率理论,假设样本为1的概率可以用sigmoid函数来表示,然后通过极大似然估计的方法估计出参数的值。支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面。 - 支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用,虽然作用会相对小一些)。
- 在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
- SVM的损失函数就自带正则!!!(损失函数中的1/2||w||^2项),这就是为什么SVM是结构风险最小化算法的原因!!!而LR必须另外在损失函数上添加正则项!!!
- SVM不是概率输出,Logistic Regression是概率输出。
总而言之,一个基于距离!一个基于概率!
Softmax Cross-Entropy 推导
为什么衡量softmax多分类的损失函数要使用交叉熵来定义,我们选取比较常用的另外的几种错误率计算:
-
Classification Error(分类错误率):无法区分分别。
-
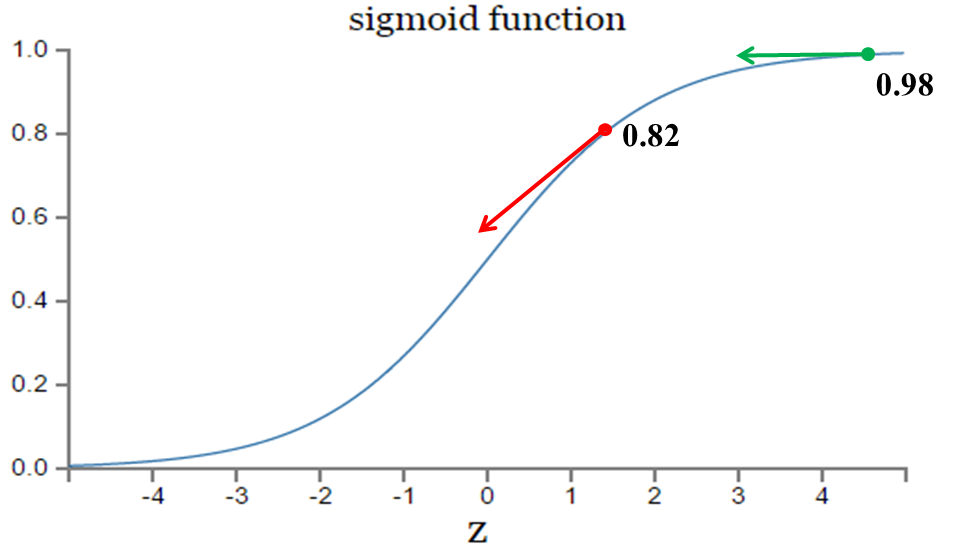
Mean Squared Error (均方误差):主要原因是逻辑回归配合MSE损失函数时,采用梯度下降法进行学习时,会出现模型一开始训练时,学习速率非常慢的情况(MSE损失函数),二次代价函数的不足,误差大的时候反而学的比较慢。
-
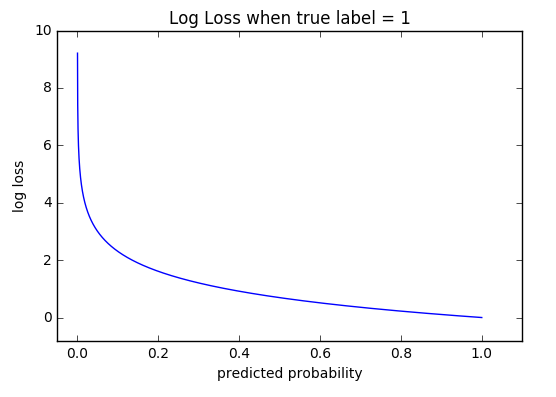
Cross Entropy Error Function(交叉熵损失函数):交叉熵函数是凸函数,求导时更容易找到全局最优解,函数的性质就比较好,因此学的也就更快。
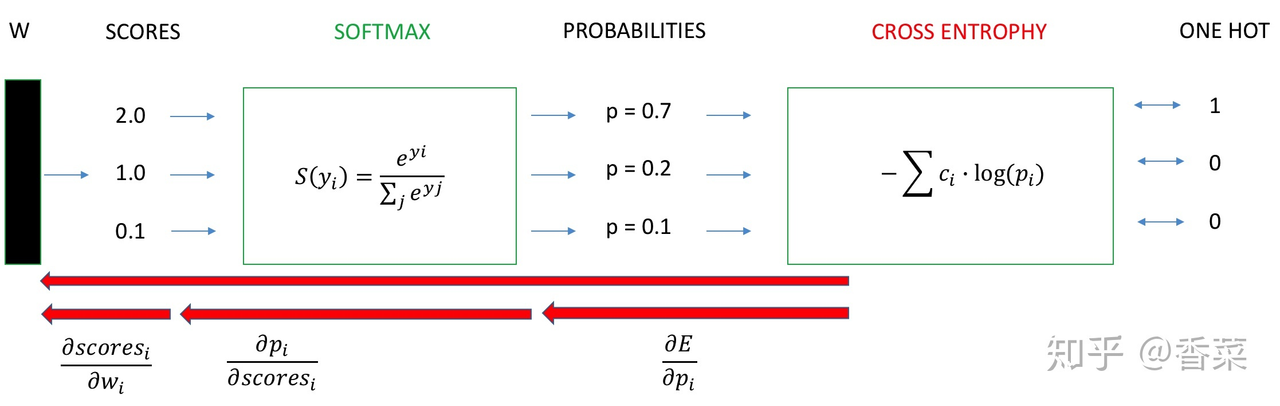
明确了交叉熵的优势后,将最后一层的网络展开,最终的结果展开成 one-hot 的形式,用 softmax 得到的概率值进行交叉熵的计算,带入公式
$$
J = - \sum _ { c = 1 } ^ { M } y _ { c } \log \left( p _ { c } \right)
$$
$$
\frac { \partial J } { \partial w _ { i } } = \frac { \partial J } { \partial p _ { i } } \cdot \frac { \partial p _ { i } } { \partial s c o r e _ { i } } \cdot \frac { \partial s c o r e _ { i } } { \partial w _ { i } }
$$
计算第一项:
$$
\begin{aligned} \frac { \partial J } { \partial p _ { i } } & = \frac { \partial - [ y \log ( p ) + ( 1 - y ) \log ( 1 - p ) ] } { \partial p _ { i } } \newline & = - \frac { \partial y _ { i } \log p _ { i } } { \partial p _ { i } } - \frac { \partial \left( 1 - y _ { i } \right) \log \left( 1 - p _ { i } \right) } { \partial p _ { i } } \newline & = - \frac { y _ { i } } { p _ { i } } - \left[ \left( 1 - y _ { i } \right) \cdot \frac { 1 } { 1 - p _ { i } } \cdot ( - 1 ) \right] \newline & = - \frac { y _ { i } } { p _ { i } } + \frac { 1 - y _ { i } } { 1 - p _ { i } } \newline & = - \frac { y _ { i } } { \sigma \left( y _ { i } \right) } + \frac { 1 - y _ { i } } { 1 - \sigma \left( y _ { i } \right) } \end{aligned}
$$
计算第二项,稍微有点复杂,第一种k等于i的情况
$$
\begin{aligned} \frac { \partial p _ { i } } { \partial s c o r e _ { i } } & = \frac { \left( e ^ { y _ { i } } \right) ^ { \prime } \cdot \left( \sum _ { i } e ^ { y _ { i } } \right) - e ^ { y _ { i } } \cdot \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { \prime } } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = \frac { e ^ { y _ { i } } \cdot \sum _ { i } e ^ { y _ { i } } - \left( e ^ { y _ { i } } \right) ^ { 2 } } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = \frac { e ^ { y _ { i } } } { \sum _ { j } e ^ { y _ { i } } } - \frac { \left( e ^ { y _ { i } } \right) ^ { 2 } } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = \frac { e ^ { y _ { i } } } { \sum _ { j } e ^ { y _ { i } } } \cdot \left( 1 - \frac { e ^ { y _ { i } } } { \sum _ { j } e ^ { y _ { i } } } \right) \newline & = \sigma \left( y _ { i } \right) \left( 1 - \sigma \left( y _ { i } \right) \right) \end{aligned}
$$
第二种考虑k不等于i的情况
$$
\begin{aligned} \frac { \partial p _ { k } } { \partial s c o r e _ { i } } & = \frac { \left( e ^ { y _ { k } } \right) ^ { \prime } \cdot \left( \sum _ { i } e ^ { y _ { i } } \right) - e ^ { y _ { i } } \cdot \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { \prime } } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = \frac { 0 \cdot \sum _ { i } e ^ { y _ { i } } - \left( e ^ { y _ { i } } \right) \cdot \left( e ^ { y _ { k } } \right) } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = - \frac { e ^ { y _ { i } } \cdot e ^ { y _ { k } } } { \left( \sum _ { j } e ^ { y _ { i } } \right) ^ { 2 } } \newline & = - \frac { e ^ { y _ { i } } } { \sum _ { j } e ^ { y _ { i } } } \cdot \frac { e ^ { y _ { k } } } { \sum _ { j } e ^ { y _ { i } } } \newline & = - \sigma \left( y _ { k } \right) \cdot \sigma \left( y _ { k } \right) \newline & = \sigma \left( y _ { k } \right) \cdot \left( 1 - \sigma \left( y _ { i } \right) \right) \end{aligned}
$$
总和两个式子的结果,我们得到了统一的形式:
$$
\frac { \partial p _ { k } } { \partial s c o r e _ { i } } = \left{ \begin{array} { l l } { \sigma \left( y _ { i } \right) \left( 1 - \sigma \left( y _ { i } \right) \right) } & { \text { if } k = i } \newline { \sigma \left( y _ { k } \right) \cdot \left( 1 - \sigma \left( y _ { i } \right) \right) } & { \text { if } k \neq i } \end{array} \right.
$$
即
$$
\frac { \partial p _ { i } } { \partial s c o r e _ { i } } = \sigma \left( y _ { i } \right) \left( 1 - \sigma \left( y _ { i } \right) \right)
$$
第三项就是直接求导
$$
\frac { \partial s c o r e _ { i } } { \partial w _ { i } } = x _ { i }
$$
综上计算统一的结果为
$$
\begin{aligned} \frac { \partial J } { \partial w _ { i } } & = \frac { \partial J } { \partial p _ { i } } \cdot \frac { \partial p _ { i } } { \partial s c o r e _ { i } } \cdot \frac { \partial s c o r e _ { i } } { \partial w _ { i } } \newline & = \left[ - \frac { y _ { i } } { \sigma \left( y _ { i } \right) } + \frac { 1 - y _ { i } } { 1 - \sigma \left( y _ { i } \right) } \right] \cdot \sigma \left( y _ { i } \right) \left( 1 - \sigma \left( y _ { i } \right) \right) \cdot x _ { i } \newline & = \left[ - \frac { y _ { i } } { \sigma \left( y _ { i } \right) } \cdot \sigma \left( y _ { i } \right) \cdot \left( 1 - \sigma \left( y _ { i } \right) \right) + \frac { 1 - y _ { i } } { 1 - \sigma \left( y _ { i } \right) } \cdot \sigma \left( y _ { i } \right) \cdot \left( 1 - \sigma \left( y _ { i } \right) \right) \right] \cdot x _ { i } \newline & = \left[ - y _ { i } + y _ { i } \cdot \sigma \left( y _ { i } \right) + \sigma \left( y _ { i } \right) - y _ { i } \cdot \sigma \left( y _ { i } \right) \right] \cdot x _ { i } \newline & = \left[ \sigma \left( y _ { i } \right) - y _ { i } \right] \cdot x _ { i } \end{aligned}
$$
因此如果反向传播的是 $i$ 对应于真实的标签为 1,即 $y_i=1$,那么回传的梯度变化就需要减去 1, 再乘以 $x_i$。如果对应真实标签为0,那么 $y_i=0$,传递回该位置的 softmax 值乘以 $x_i$。如此一来,我们就得到了全连接层到输出层的梯度变化了,再回传其实也没有那么困难了。
总结
LR 和 Softmax 是一切机器学习的基础,推导完毕后发现,其实两者还是存在很多的共性,尤其从结论来看,都是(真实-预测)* 输入,但是这个结论的得来要归功于 sigmoid 函数和 softmax 函数良好的凸性,梯度随误差增大而增大,以及易于求导三方面因素共同决定的,也佩服于先人的才学,才有了今天的发展。
参考:
https://www.jianshu.com/p/dce9f1af7bc9
https://zhuanlan.zhihu.com/p/35709485
https://zhuanlan.zhihu.com/p/25723112