Leetcode-70 爬楼梯问题(DP)
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
一道经典的爬楼梯问题,直觉上第一个想到的就是采用递归,也就是要计算爬到第3层楼梯有几种方式,可以从第2层爬1级上来,也可以从第1层爬2级上来,所以爬到第3级有几种方式只需要将到第2层总共的种数,加上到第1层总共的种数就可以了。推广到一般,写出递推公式
$stairs(n) = stairs(n-1) + stairs(n-2) $,只需要初始化好退出递归的条件就算写完了。
方法1,直接采用递归。
class Solution:
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n <= 1:
return 1
if n == 2:
return 2
return self.climbStairs(n - 1) + self.climbStairs(n - 2)
然而,没有AC (ーー゛),理由是超时。这就引出了在递归里经常会采用的备忘录法,因为这里面同一个n被重复计算了n次,因此一定程度上影响了性能,比如stairs(5) = stairs(4) + stairs(3), stairs(4) = stairs(3) + stairs(2),stairs(3)就被计算了2次,因此借助一个字典存储计算过的值,就可以大大减少重复的计算了,就诞生了备忘录形式的递归。
方法2,备忘录递归
class Solution:
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
refs = dict() # 建立字典类型备忘录
def rec(n):
# 初始条件写入备忘录
if n <= 1:
refs[n] = 1
return 1
if n == 2:
refs[n] = 2
return 2
# 存在于字典的直接输出
if n in refs:
return refs[n]
else:
refs[n] = rec(n - 1) + rec(n - 2)
return refs[n]
return rec(n)
这次AC了,︿( ̄︶ ̄)︿
既然都已经做到备忘录了,那其实和动态规划也就没有什么两样,递归采用自顶向下,动态规划采用自底向上,借助一个数组来加以实现,要计算n阶就往对应数组里插入到n阶。
方法3,动态规划
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
res = [1, 1, 2] #初始化
if n >=3:
for i in range(3, n + 1):
res.append(res[i - 1] + res[i - 2])
return res[n]
也是AC的,\( ̄︶ ̄)/
不难发现,这个递推公式有点像Fibonacci数列,其实就是Fibonacci数列。。。因此也可以借助Fibonacci数列递推的思想直接就可以写出来了。
方法4,Fibonacci递推
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n <= 1:
return 1
if n == 2:
return 2
if n >= 3:
first, second = 1, 2
for i in range(3, n + 1):
third = first + second
first = second
second = third
return second
比较简单和基础的一道题,以上
leetcode-242 重排校验
Given two strings s and t , write a function to determine if t is an anagram of s.
Example 1:
Input: s = “anagram”, t = “nagaram”
Output: true
要满足重排,就一定要含有相同个数的字幕,那么就可以转化成 list of chars,看每一个sort过后的list是否相同就可以了。
写一个最简单的排序方法
class Solution:
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
origin = sorted(list(s))
current = sorted(list(t))
return origin == current
另外就是可以尝试一下Counter这种计数器的方法。虽然这个方法挺不要脸的,利用Counter直接生成一个hashmap。
from collections import Counter
class Solution:
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
return Counter(s) == Counter(t)
leetcode-104 二叉树最大深度
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Note: A leaf is a node with no children.
Given binary tree [3,9,20,null,null,15,7],return its depth = 3.
直觉上,看例子以为是要用数组来做,但是应该是用树。用DFS的思想借助递归实现,(重点: 树的题一般都要用递归来解决),先递归左子树,层层深入下去,注意一点在python中,
max(0, None) = 0
也就意味着,对某个节点,如果左节点叶子存在,右节点叶子不存在为None的话,这时max()函数取值也为0。
整理得出如下:
class Solution:
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
else:
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height, right_height) + 1
leetcode-160 链表交集
Write a program to find the node at which the intersection of two singly linked lists begins.
For example, the following two linked lists:
A: a1 → a2
↘
c1 → c2 → c3
↗
B: b1 → b2 → b3
begin to intersect at node c1.
链表题用指针,或者双指针还是挺常用的方法。有看到说用字典来存储的,感觉虽然能解决问题,但是一定程度上破坏了链表的数据结构。分析题目,大概有那么2个思路。
- 指针顺序遍历,解决一个问题就是2个链表长度不同,所以第一步要遍历得到2个链表的长度(这块可能空间复杂度开销比较大)。将长链表向前移动至剩余链表长度与短链表一致。
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def getIntersectionNode(self, headA, headB):
"""
:type head1, head1: ListNode
:rtype: ListNode
"""
if headA == None or headB == None:
return None
len_a, len_b = 0, 0
# 赋值计算长度
p, q = headA, headB
while p:
p = p.next
len_a += 1
while q:
q = q.next
len_b += 1
# 赋值截断到相同长度
p, q = headA, headB
if len_a > len_b:
for i in range(len_a - len_b):
p = p.next
else:
for i in range(len_b - len_a):
q = q.next
while p != q:
p = p.next
q = q.next
return p
- 最大的障碍是2个链表长度不同,所以有一个巧妙的办法来补齐。就是当一个链表先行到达链表尾部时,将Next指针去指向另一个链表的头部,同理另一个链表也同样如此,这样就保证了在O(m+n)内一定能找到结果。举个例子:
ListNodeA = 0, 9, 1, 2, 4
LIstNodeB = 3, 2, 4
Path of A -> B = 0, 9, 1, 2, 4, 3, 2, 4
Path of B -> A = 3, 2, 4, 0, 9, 1, 2, 4
这样只需要遍历一次,如果遍历结束2个指针仍然不同都指向None,也就没有交集.
class Solution(object):
def getIntersectionNode(self, headA, headB):
"""
:type head1, head1: ListNode
:rtype: ListNode
"""
p, q = headA, headB
while p != q:
p = headB if p is None else p.next
q = headA if q is None else q.next
return p
Leetcode-204 质数个数
Count the number of prime numbers less than a non-negative number, n.
Example:
Input: 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
乍一看以为应该没什么的题目,结果写了一版,先是边界条件也写好,再就是TLE感觉过不去了。先来一个基本方法吧,毕竟我不可能在实战中短时间想到一个fancy的方法。
import math
class Solution:
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
import math
count = 0
# 一个判断是否为质数的方法
def judge_prime(w):
sqrt_w = int(math.sqrt(w))
# 迭代相除直到sqrt(w)
# 注意传入2时,sqrt(2) + 1 = 2, range(2, 2)不会执行,因此还是会返回1
# 不然边界条件太乱了。
for i in range(2, sqrt_w + 1):
if x % i == 0:
return 0
return 1
for x in range(2, n):
count = count + judge_prime(x)
return count
但是这个方法没有在Leetcode上AC,主要还是太慢了。
看了网上的大神介绍了一个厄拉多塞筛法(Sieve of Eeatosthese)。先上代码,
def countPrimes(self, n):
if n < 3:
return 0
primes = [True] * n
primes[0] = primes[1] = False
for i in range(2, int(n ** 0.5) + 1):
if primes[i]:
primes[i * i: n: i] = [False] * len(primes[i * i: n: i])
return sum(primes)
对着代码解释下大概的思想是:
- 创建一个数组,长度为n个True,第0,1个位置设置为False,即0和1不是质数。
- 从2开始(True,初始化),用2举例,以2*2作为起点开始迭代,迭代的终点是n,步长为2,将满足的都标记为False。
- 同理3,4由于已经被2标记了跳过,5同理,6被标记,7同理,循环的终点就是$\sqrt{n}$。这里解释一下,因为一共有n个数,每次的起点是i*i,这是因为避免了重复的计算,比如3是从3*3开始的,因为3*2已经计算过了,$\sqrt{n} * \sqrt{n}$作为终点也是保证了不重复计算。总的遍历从2到$\sqrt{n}$,次数下降了指数级别。
- 这里又借助了python list的可以设置变步长的性质 [i*i : n : i],也不需要额外开辟更大的空间,可以说是时间复杂度和空间复杂度都做到了极致。
- AC了,但是凭空我肯定是想不到的。
Leetcode-17 Letter Combinations of a Phone Number 字母组合
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
其中按键对应的字母映射要自己建一个dictionary,汗。。。如下:
(letters = {‘2’: ‘abc’, ‘3’: ‘def’, ‘4’: ‘ghi’, ‘5’: ‘jkl’,
‘6’: ‘mno’, ‘7’: ‘pqrs’, ‘8’: ‘tuv’, ‘9’: ‘wxyz’})
Input: “23”
Output: [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
这个题乍一看,典型的递归,深度遍历的长相,于是乎,开始写了起来,毕竟是递归嘛,脑子大概想着要有一个重复子问题。也差不多想到了就是每一次迭代都要拿上一次的结果,拼接上新一次的字母,而且这个拼接要是一个组合,所以总体来说规模是要逐步扩大的。因此,既然要扩大,应该是在for循环里套一层递归的大概样子。写了一个大概的版本,尽然AC了。。。猝不及防
class Solution:
def letterCombinations(self, digits):
"""
:type digits: str
:rtype: List[str]
"""
letters = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
def dfs(res, index):
new_lts = [i for i in letters[input[index]]]
res = [i + j for i in res for j in new_lts] # 拼接生成最新的结果
index += 1
# 递归结束标志
if index > len(input) - 1:
return res
else:
return dfs(res, index) 每次传入当前结果,以及下一个新的数字键
input = list(digits)
如果输入为空,则返回空。
if len(input) < 1:
return []
# 初始化从1开始
initial = [i for i in letters[input[0]]]
idx = 1
if len(input) == 1:
return initial
return dfs(initial, idx)
但是这个递归是写的有点问题的,其实似乎就有点不像个递归了。原因在于因为递归是把复杂问题化小,递归到越来越简单的规模。而我这里只是借助了一个递归来传递我每一次新的值给下一个数字键,既然是传递,那其实可以直接写for循环来实现的,于是我改了改:
class Solution:
def letterCombinations(self, digits):
"""
:type digits: str
:rtype: List[str]
"""
letters = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
input = list(digits)
if len(input) < 1:
return []
comb = [i for i in letters[input[0]]]
for num in input[1:]:
comb = [i + j for i in comb for j in letters[num]]
return comb
这样改写之后,就比我之前的第一种顺眼多了。这里的技巧就是循环重复更改结果,第一种里的res和第二种里的comb。
而真正使用递归来求解,我参照了一下大神的标准答案,很巧妙运用了化繁为简的策略,这里运用了一个小技巧就是使用了list的[:-1]来递归前一种情况。也就是说本来比如输入5个数字,那递归到第5次得到的结果就是前4次加上第5次的,那第4次就是前3次加第4次的,以此类推。递推公式为
$$comb(n) = F(\ comb(n-1),\ curr(n)\ )$$
其中$F()$函数就是求组合数,这样想了一下就可以写了如下:
class Solution:
# @param {string} digits
# @return {string[]}
def letterCombinations(self, digits):
mapping = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
if len(digits) == 0:
return []
if len(digits) == 1:
return list(mapping[digits[0]])
prev = self.letterCombinations(digits[:-1])
# additional就是current
additional = mapping[digits[-1]]
return [s + c for s in prev for c in additional] #生成新的组合
Leetcode-455 Assign Cookies 分配饼干
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie. Each child i has a greed factor gi, which is the minimum size of a cookie that the child will be content with; and each cookie j has a size sj. If sj >= gi, we can assign the cookie j to the child i, and the child i will be content. Your goal is to maximize the number of your content children and output the maximum number.
Note:
You may assume the greed factor is always positive.
You cannot assign more than one cookie to one child.
Example 2:
Input: [1,2], [1,2,3]
Output: 2
Explanation: You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
直觉上,这题也太tm简单了吧,拿每个小孩出来比一下,存在就计数加1,饼干顺势干掉1块,循环完然后输出结果,但是报错,发现自己忽略了一个重要的条件,要最多分配给别的小孩。好,那我就饼干选小孩吧,多一个差值位来记录饼干和小孩要求的差距,如果等于0立马输出,如果循环结束都没有等于0,那就选择给差值最小的那个小孩,可能比较丑陋,不过肯定是可以实现的,就写了下来:
class Solution:
def findContentChildren(self, g, s):
"""
:type g: List[int]
:type s: List[int]
:rtype: int
"""
#先检查边界
if len(g) == 0 or len(s) == 0:
return 0
count = 0
for ck in s:
tmp = ck
for px in g:
if ck >= px and (ck - px <= tmp):
tmp = ck - px
if tmp == 0: #等于0,立刻跳出开始下一个
count += 1
g.remove(px)
break
if tmp < ck and tmp != 0:
g.remove(ck - tmp)
count += 1
return count
但是,很显然这个方法时间复杂度$O(n^2)$是一定会TLE的。于是想下一个方法,很自然的就是需要对原始数组进行排序,这样就不用存储中间结果了,可以顺序的往下执行。
class Solution:
def findContentChildren(self, g, s):
"""
:type g: List[int]
:type s: List[int]
:rtype: int
"""
#先检查边界
if len(g) == 0 or len(s) == 0:
return 0
count = 0
g.sort()
s.sort()
for ck in s:
for px in g:
if ck >= px:
count += 1
g.remove(px)
break
return count
AC了,也可以借助双指针,主指针是饼干,从动的那个指针是小孩,这样就可以省去异常值也放进去循环了,差不多的思想,排序之后其实优化方法还有很多,感觉排序就是一个能让天空放晴的办法,借助while和指针,大概写了一下:
class Solution:
def findContentChildren(self, g, s):
"""
:type g: List[int]
:type s: List[int]
:rtype: int
"""
#先检查边界
if len(g) == 0 or len(s) == 0:
return 0
g.sort()
s.sort()
ckp, chp = 0, 0
while ckp < len(s) and chp < len(g):
if s[ckp] >= g[chp]:
chp += 1
ckp += 1
return chp
巧妙。
Leetcode-416 Partition Equal Subset Sum 分割相等子集
Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
Note:
Each of the array element will not exceed 100.
The array size will not exceed 200.
Example 1:
Input: [1, 5, 11, 5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
经典题,说实话写这个题花了不少时间,尤其是想清楚这个里外里的道理。这道题是一道典型的背包问题,但是在成为背包问题之前,要做一些必要的转换。
- 首先,题目要求2个子数组和相等,因此,只有大数组的和为偶数,才可能使得2个子数组和是相等,所以一旦和为奇数就可以立即排除输出
False。 - 其次对于和为偶数的情况,可以将总和除2作为每个子数组的目标和,所以问题就转化为找出子数组和为$target = sum / 2$。
- DP问题就是要借助DP的思想,就要写一下状态转移方程,作为写代码的指导思想。动态规划都是借助一个2维或者1维的表格来建立整个过程,于是我们借一个例子来画一下表格:
0 1 2 3 4 5 6 8 9 10 11
0 1 0 0 0 0 0 0 0 0 0 0
1 1 1 0 0 0 0 0 0 0 0 0
5 1 1 0 0 0 1 1 0 0 0 0
5 1 1 0 0 0 1 1 0 0 0 1
行表示每一个数,列表示能够达到所有可能的和(这里可以记忆一下,DP问题是由繁化简,所以一定是有状态从最起始开始一直到我们的目标,在例子中起始为0,目标是11,中间所有可能的值也都要考虑,这点和背包问题是一样的)。由于我们现在的问题是数组和能否达到某个固定的数,因此可以写得递推公式为$dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]$。
稍微解释一下这个公式,第一项$dp[i-1][j]$是说,如果上一行(i-1)已经满足和为j了,那下一行也一定会满足和为j,所以i项不加也可以满足,状态照搬下来就可以,就好比01背包问题,不取当前项,最大价值仍然延续上一个状态一个意思。而$dp[i-1][j-nums[i]]$表示前i-1个数,在target - nums[i
]处已经满足,那加上nums[i]也同样会满足,显示了DP的递推性。这样主体就搭建好了。
在这里也要注意一下初始值的问题,j为0意味着和为0,也就是不取任何数,所以dp[:][j=0]要设置为True(一个都不取,什么都不用做就满足了,也是强)。于是就可以写下代码了:
class Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if sum(nums) % 2 == 1:
return False
target = sum(nums) // 2
# dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]
dp = [[False for i in range(target + 1)] for j in range(len(nums) + 1)]
dp[0][0] = True
for i in range(1, len(nums) + 1):
for j in range(1, target + 1):
dp[i][j] = dp[i-1][j]
if j >= nums[i-1] and dp[i-1][j-nums[i-1]]:
dp[i][j] = True
return dp[-1][-1]
这里有可以改进的地方,就是原始是采用了一个二维数组来存储数据的,其实可以优化为一维数组的,这一点和背包问题是一致的,需要注意的是内层的遍历要降序遍历,来防止对已经生成的数据做重复修改,不展开了,可以参考背包问题整理(二维转一维数组)。改写如下:
class Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if sum(nums) % 2 == 1:
return False
target = sum(nums) // 2
# dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]
dp = [False for i in range(target + 1)]
dp[0] = True
for i in range(0, len(nums)):
for j in range(target, nums[i] - 1, -1):
dp[j] = dp[j] | dp[j - nums[i]]
return dp[-1]
这题有用别的奇技淫巧来解的,我就不推荐了,主要还是可以借机会复习01背包动态规划的思想,以及转移状态的确定和思维的转换。其他大神的办法无非是在DFS上做文章,我是真的想不到,就老老实实的吧,毕竟慢学。
Leetcode-215 第K个最大的数
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
Example 1:
Input: [3,2,1,5,6,4] and k = 2
Output: 5
这道题聊解题没有任何意义,主要是周末想借这个机会复习一下所有的排序算法思想,先给个最简单的题解吧。
class Solution:
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
nums.sort(reverse=True)
return nums[k - 1]
这里顺便复习几个比较常用的排序算法:冒泡,选择,插入,归并,快排。
冒泡:
class Solution:
def findKthLargest(self, nums, k):
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[j] > nums[i]:
nums[i], nums[j] = nums[j], nums[i]
return nums[k-1]
选择:
class Solution:
def findKthLargest(self, nums, k):
for index in range(len(nums)):
tmp = index
for j in range(index + 1, len(nums)):
if nums[j] > nums[tmp]:
tmp = j
nums[index], nums[tmp] = nums[tmp], nums[index]
return nums[k - 1]
插入,这个还是想了一下的,主要是用while的话更加清楚一些。
class Solution:
def findKthLargest(self, nums, k):
for i in range(1, len(nums)):
key = nums[i]
j = i - 1
while j >= 0 and nums[j] < key:
# 只要key比已排序好的数大,先对原数进行移位操作,腾出空间。
nums[j + 1] = nums[j] #会有个重复
j -= 1
# while条件不满足时,这里nums[j + 1]其实是(j - 1) + 1 = j,将key置于上步腾出的那个位置
nums[j + 1] = key
return nums[k-1]
归并:
class Solution:
# 2. 再对left和right作归并排序
def merge_sort(self, left, right):
i, j = 0, 0
result = []
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
# 1. 先拆分,运用递归
def divide_merge(self, nums):
if len(nums) <= 1:
return nums
num = len(nums) // 2
left = self.divide_merge(nums[:num])
right = self.divide_merge(nums[num:])
return self.merge_sort(left, right)
def findKthLargest(self, nums, k):
res = self.divide_merge(nums)
return res[-k]
快排:
class Solution:
def findKthLargest(self, nums, k):
pivot = nums[0]
left = [l for l in nums if l < pivot]
equal = [e for e in nums if e == pivot]
right = [r for r in nums if r > pivot]
if k <= len(right):
return self.findKthLargest(right, k)
elif (k - len(right)) <= len(equal):
return equal[0]
else:
return self.findKthLargest(left, k - len(right) - len(equal))
这里面比较难想的是插入,归并和快排,有必要做一个专题来攻克一下。虽然以前也学过,而且说来说去也大概知道原理,但是真正自己实现的时候,还是没有那么快能解决。
Leetcode-46 Permutations 排列
Given a collection of distinct integers, return all possible permutations.
Example:
Input: [1,2,3]
Output:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
一道经典的回溯题,看到这样的例子,第一反应就是用DFS搭配回溯,既然是深度优先遍历,一般会用一个visited来记录遍历到的位置,运用for加递归的方式进行遍历,设置退出的条件。回溯算法需要将visited的状态回退,这里运用了一个pop方法将栈中的元素末尾弹出后回溯到上一层状态。这里因为是for循环加上递归的结构,递归其实可以看成是一个一般的函数调用(有返回值),当次的for循环结束后,弹出末尾元素,下一次循环后再压入,以此往复。
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
def helper(nums, visited):
if len(visited) == len(nums):
res.append(visited[:])
for item in nums:
# 如果已经存在就不再记入
if item in visited:
continue
visited.append(item)
helper(nums, visited)
visited.pop()
helper(nums, [])
return res
AC了,看到另外的解法,避免了在循环中进行判断,而是在传入下层递归的时候,就只传入除去当次循环的那个元素后的剩余元素,要巧妙的多。
class Solution(object):
# DFS
def permute(self, nums):
res = []
self.dfs(nums, [], res)
return res
def dfs(self, nums, path, res):
if not nums:
res.append(path)
# return # backtracking
for i in range(len(nums)):
self.dfs(nums[:i]+nums[i+1:], path+[nums[i]], res)
Leetcode-647 Palindromic Substrings 回文子串个数
Given a string, your task is to count how many palindromic substrings in this string.
The substrings with different start indexes or end indexes are counted as different substrings even they consist of same characters.
Example 1:
Input: “abc”
Output: 3
Explanation: Three palindromic strings: “a”, “b”, “c”.
Example 2:
Input: “aaa”
Output: 6
Explanation: Six palindromic strings: “a”, “a”, “a”, “aa”, “aa”, “aaa”.
经典题,求回文子串个数,应该只要循环加递归就可以搞定了,理一下思路:回文的特征就是以某一个中心位置为轴对称,但是这里有一点要注意就是奇数个子串有中心位置,但是偶数个数的子串中心位置应该是两个数。明确了这一点之后,循环到某一个位置时,设置两个指针i和j分别从中心位置++和–,直到任何一个指针到达边界小于0或超过数组长度截止,如果有满足 s[i] == s[j] 就继续迭代进行。思路不难,实现了一下:
class Solution:
def __init__(self):
self.count = 0
def countSubstrings(self, s):
"""
:type s: str
:rtype: int
"""
def move_check(input, i, j):
if i < 0 or j >= len(input):
return
if input[i] == input[j]:
self.count += 1
else: # 不满足及时跳出,有效减少无效递归。
return
i -= 1
j += 1
move_check(input, i, j)
index = 0
while index < len(list(s)):
move_check(list(s), index, index) #奇数
move_check(list(s), index - 1, index) #偶数
index += 1
return self.count
AC了,看了个大神的方法,用了for嵌套while的结构,看着还是挺清楚的,我承认我之前非要写个递归,其实就是想自己练练写递归,也没什么特别的道理哈哈。这里用了一个技巧来一步实现奇数偶数的判断,left = center / 2, right = center / 2 + center % 2. 实现如下:
class Solution:
def countSubstrings(self, S):
N = len(S)
ans = 0
for center in range(2*N - 1):
left = center // 2
right = left + center % 2
while left >= 0 and right < N and S[left] == S[right]:
ans += 1
left -= 1
right += 1
return ans
Leetcode-230 Kth Smallest Element in a BST BST树中第k个最小值
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
Note:
You may assume k is always valid, 1 ≤ k ≤ BST’s total elements.
Example 1:
Input: root = [3,1,4,null,2], k = 1. Output: 1
3
/
1 4
2
最近翻看了很多树类的题目,凡是见到树的题目,脑子就要有一个递归的大体框架,如果递归比较弱的,比如我自己,就可以有针对性的练几个树的题目提高一下。
这一题,乍一看也挺简单的,直觉上利用BST树的基本性质,左小右大,于是写了一个遍历左子树的递归,但是报错,这才发现如果K值过大的话,还是需要右子树的,会觉得需要对K做分情况考虑了一下子好像觉得有点复杂了。而像这种第几个XXX的题目,排序似乎永远都是一个不错的方案,全局排序会导致较大的时间开销,设置条件提前停止是一个比较不错的优化方案。
由于每一棵树都是左>根>右,因此采用中序遍历(LDR)代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def kthSmallest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
vals = [] # 初始化一个数组
def ldr(node):
if node is None:
return
dfs(node.left)
vals.append(node.val)
dfs(node.right)
ldr(root)
return vals[k - 1]
为了训练,也可以用非递归的形式来解,但是这边需要,我这里练习并记录一下
class Solution:
def kthSmallest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
stack = [] # stack以栈来放置node,到达放入,结束后弹出
node = root # node用来表示当前的节点
res = [] # 存放排序结果
while node or stack:
while node:
stack.append(node) # 插入当前节点
node = node.left
node = stack.pop() # 弹出最底层的节点
res.append(node.val)
node = node.right
return res[k - 1]
这里的两个方法,其实都只是直接考虑全局排序的,时间消耗是很大的,从AC后的耗时可以看出,要优化的话,就要从这个k入手,记录并精准返回第k个然后程序结束。写一下:
class Solution:
def kthSmallest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
self.k = k
self.res = None
self.helper(root)
return self.res
def helper(self, node):
if not node:
return
self.helper(node.left)
self.k -= 1 # 计数并精准返回
if self.k == 0:
self.res = node.val
return
self.helper(node.right)
Leetcode-69 Sqrt(x) 开根号
Implement int sqrt(int x).
Compute and return the square root of x, where x is guaranteed to be a non-negative integer.
Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.
Example 1:
Input: 4
Output: 2
一道简单题,python可以导入math,或者用x**都可以得到结果,但是这不是目的。这是一题二分查找的题,考虑了一些边界条件和结束条件,就写了如下的一个方法,有点繁杂但是可以AC:
class Solution:
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
if x == 0:
return 0
def calculate(i, j, x):
if i * i == x:
return i
if j * j == x:
return j
if j - i <= 1:
return i
mid = (i + j) // 2
if mid * mid > x:
return calculate(i, mid, x)
else:
return calculate(mid, j, x)
return calculate(1, x, x)
我是故意写递归的,目的是让自己习惯。下面照着大神的做法,理解了写了个别的方法
class Solution:
def mySqrt(self, x):
l, r = 0, x
while l <= r:
mid = l + (r-l)//2
if mid * mid <= x < (mid+1)*(mid+1):
return mid
elif x < mid * mid:
r = mid
else:
l = mid + 1
这里巧妙的在于,初始是0也就不需要额外判断了,然后把我上面的三个条件并成了一个,如果x在mid*mid和(mid+1) *(mid+1)之间即输出。不过这个题,只要想到二分查找就至少答到题意了,有些优化可能第一时间想不到也没关系。就这样吧。
Leetcode-226 Invert Binary Tree 翻转二叉树
Invert a binary tree.
Example:
Input:
4
/
2 7
/ \ /
1 3 6 9
Output:
4
/
7 2
/ \ /
9 6 3 1
这个题来源于一个小故事,Google: 90% of our engineers use the software you wrote (Homebrew), but you can’t invert a binary tree on a whiteboard so f*** off. 哈哈哈。这个题也是一个典型树类的递归应用,直接交换左右子树位置就好了。代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if not root:
return None
# tmp = root.left
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
还可以进一步简化为这样子:
class Solution:
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if root:
invert = self.invertTree
root.left, root.right = invert(root.right), invert(root.left)
return root
反正也是一个意思吧。
总体来说,树类的问题套路一般就是直上直下的遍历,采用递归或者while的循环都可以,遍历的3种模式中,前序遍历,中序遍历可以相互转化,后序遍历和层次遍历(BFS)可以一起记忆。另一类就是DFS,需要维护和记录一个visited数组。
Leetcode-435 Non-overlapping Intervals 不重复交集
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note:
You may assume the interval’s end point is always bigger than its start point.
Intervals like [1,2] and [2,3] have borders “touching” but they don’t overlap each other.
Example 1:
Input: [ [1,2], [2,3], [3,4], [1,3] ]
Output: 1
Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.
这种题目,其实不难,但是如果一旦想偏了,就很难做对了。这里的问题是他有一个假设条件可以简化运算,就是每个interval是按大小排好的。然后这个题的trick就是可以做一次排序,这样可以避免两层的for循环嵌套,而且每个interval的关系定下了一层遍历更加清楚,其实这个已经想到了,只是一开始控制条件没有写对,耽误了很多时间。思路:记录一个end指针,如果下一个start >= current_end,就更新这个end指针,否则就记录一个overlap,代码如下:
# Definition for an interval.
# class Interval(object):
# def __init__(self, s=0, e=0):
# self.start = s
# self.end = e
class Solution(object):
def eraseOverlapIntervals(self, intervals):
"""
:type intervals: List[Interval]
:rtype: int
"""
if len(intervals) <= 1:
return 0
intervals.sort(key = lambda x: x.end)
start, current_end = intervals[0].start, intervals[0].end
count = 0
for item in intervals[1:]:
if item.start >= current_end:
current_end = item.end
else:
count += 1
return count
AC了,这个题没什么特别的,就是要一开始想清楚。
Leetcode-51 N-Queens N皇后
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other. Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.
Example:
Input: 4
Output: [
[“.Q…”, // Solution 1
“…Q”,
“Q…”,
“…Q.”],
[“…Q.”, // Solution 2
“Q…”,
“…Q”,
“.Q…”]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.
我觉得是一道必须掌握的难题,八皇后考验了整体的思维,我个人也想了很多,推倒了重来了好几次。
第一先审题,这里的问题是说要返回所有可能的解,而不是只是返回一个可能的解。这一点我折腾了很久,写完了发现有点问题。
第二,开始想模块,我不可能像大牛们可以一下子一步到位输出结果,所以想把每一个模块列出来:
- 判断模块,3个情况,不在同一行,不在同一列,不在同一个斜线。这里的斜线要考虑2个方向:abs(r1-r2) == abs(c1 - c2)以及 r1+c1 == r2+c2 (checkValid())。
- 主模块,递归加遍历,这里我比较优先采用DFS来收集(dfs())。
- 打印结果模块 (trans_print())。
class Solution:
def __init__(self):
self.res = []
def checkValid(self, current, visited):
if not visited:
return True
curr_row = len(visited)
# 三个情况的判断
for idx, item in enumerate(visited):
if abs(item - current) == abs(idx - curr_row) or (idx + item) == current + curr_row or current == item:
return False
return True
def dfs(self, visited, n):
if len(visited) == n:
self.res.append(visited) # 结果收集
return
for col in range(n):
if self.checkValid(col, visited):
self.dfs(visited + [col], n) #!这里需要格外注意,只有visited +
#[col]这样可以支持程序回退
def trans_print(self, res, n):
if not res:
return []
final_res = []
for r in res: # 结果打印
res_list = []
for num in r:
temp = ['.'] * n
temp[num] = 'Q'
res_list.append(''.join(temp))
final_res.append(res_list)
return final_res
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
self.dfs([], n)
return self.trans_print(self.res, n)
我这里是写的比较啰嗦的,其实是为了看的清楚一些,其中很关键的一点是visited + [col],不能直接写生visited += [col],因为在下一次传递参数的时候,不成功不会改变visited的值,这样做可以简化我们的回退操作,比如我们一直递归下去会出现visited + [col] + [col] + [col],一旦这时条件判断不成立需要回退,那么我们仍然可以退回到上一次的遍历即visited + [col] + [col]。这个技巧我看该题的Discussion里也都是这样做的。另外贴一下大神的解法:
def solveNQueens(self, n):
def DFS(queens, xy_dif, xy_sum):
p = len(queens)
if p==n:
result.append(queens)
return None
for q in range(n):
if q not in queens and p-q not in xy_dif and p+q not in xy_sum:
DFS(queens+[q], xy_dif+[p-q], xy_sum+[p+q])
result = []
DFS([],[],[])
return [ ["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in result]
他这里用到的方法和我也比较类似,也是只存储列的值,行值用index表示,巧妙地在于传递的是累加的验证条件,还有最后的打印结果都是值得学习的地方。
Leetcode-19 Remove Nth Node From End of List 末尾移除节点
Given a linked list, remove the n-th node from the end of list and return its head.
Example:
Given linked list: 1->2->3->4->5, and n = 2.
After removing the second node from the end, the linked list becomes 1->2->3->5.
我其实觉得链表题我挺抓不到感觉的,很多时候都觉得遇到会就是会,不想别的题,怎么都能有个思路。这一题就是一道典型的快慢指针题,问题是删除末尾第N个,所以当快指针到达链表尾部,对应删除重新定义慢指针的Next元素就基本搞定了:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
ahead, behind = head, head
mark = n
while mark > 0:
ahead = ahead.next
mark -= 1
if not ahead:
return head.next
while ahead.next:
ahead = ahead.next
behind = behind.next
behind.next = behind.next.next
return head
如果N大于等于了我们链表的长度,也就是要删除链表头部的结点了,这是就直接把头结点砍掉,返回剩下的就可以了,这是属于边界条件的考察,需要注意。
Leetcode-235 Lowest Common Ancestor of a Binary Search Tree BST最低公共祖先
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
题目是一道BST的题,一看到BST题就要想到左小右大的性质,一般树类的问题都是采用递归,这题也不例外,分析题目:给定P和Q,要找到其最低的公共祖先,公共祖先也可以为它自己本身。条件可以得知自顶向下遍历,如果落在P和Q之间就为其公共祖先,反之则要通过最大和最小值来进行判断,如果root值已经大于P和Q的最大值,则将左子树带入递归遍历,如果root值小于P和Q最小值,则将右子树带入递归遍历。代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
max_num = max(p.val, q.val)
min_num = min(p.val, q.val)
if root.val >= min_num and root.val <= max_num:
return root
if root.val > max_num:
return self.lowestCommonAncestor(root.left, p, q)
else:
return self.lowestCommonAncestor(root.right, p, q)
贴个大神方法:
def lowestCommonAncestor(self, root, p, q):
a, b = sorted([p.val, q.val])
while not a <= root.val <= b:
root = (root.left, root.right)[a > root.val]
return root
这里用[a > root.val]来选择左右子树,成立则为True, True就是1,则指向右子树。繁殖False为0,传入左子树,哈哈哈,算是个小小的骚操作吧。总之还是比较送分的一题。
Leetcode-207 Course schedule
There are a total of n courses you have to take, labeled from 0 to n-1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
Example 1:
Input: 2, [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
Example 2:
Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should
also have finished course 1. So it is impossible.
又是一道并不简单的拓扑排序题,是一个检测是否为DAG的问题。由于课程和课程之间形成了依赖,所以如果我们要能成功选择所有的课,那么就意味着所有课之间的依赖不能有环,也就是不能循环依赖。所以我们可以用图来表示整个过程,类似于这样
要表示这个图,我们当然可以采取如题示的那样每一个边都独立表示,但是那样实在是不够直观,因此借助图论的知识,我们用顶点(vertice)建立字典来存储整个数据结构,上述的图就可以表示为
# out(出顶点) -> in(入顶点)
{
0: [1, 2],
1: [3],
2: [3]
}
# in(入顶点) -> out(出顶点)
{
1: [0],
2: [0],
3: [1, 2]
}
有了图的表示之后,就自然引出了2个非常经典的拓扑排序解法,一个是BFS,一个是DFS。
先说BFS,由于图的表示,让BFS不那么的直观,直觉都会想着去顺着有向图来遍历,我一开始也在想这东西怎么做BFS,网上搜到了一个kahn’s算法,读了一下立马就直观多了:
其实就是不断的寻找有向图中没有前驱(入度为0)的顶点,将之输出。然后从有向图中删除所有以此顶点为尾的弧。重复操作,直至图空,或者找不到没有前驱的顶点为止。
该算法还可以判断有向图是否存在环(存在环的有向图肯定没有拓扑序列),通过一个count记录找出的顶点个数,如果少于N则说明存在环使剩余的顶点的入度不为0。(degree数组记录每个点的入度数)
基本有了一个概念之后,就要来着手自己实现了,首先明确需要借助的存储空间,为了直观我大概列了三个:
- 入度为0的顶点的集合(每次遍历图,如果图顶点的后继节点不存在,那就移入入度为0的集合)
- 遍历过已经放入的结果集(遍历过的放入结果中)
- 当前图(字典,当移除入度为0的顶点,同步也要将图中的边进行更新,同步移除包含该入度为0顶点对应的边,再进行判断,如果移除后顶点本身同样没有进入的边了即值为空数组,便也要将其更新到入度为0顶点的集合中,以便继续遍历结束)。
结束的条件就是最终我们能否将整个图都消灭完毕,如果不能则证明图中含有环。
我依旧自己先比较丑陋的实现了一下:
class Solution:
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
ordered = [] # 存结果
graph = collections.defaultdict(list) #表示图
for out, into in prerequisites:
graph[into].append(out)
zero_in_degree = [i for i in range(numCourses) if i not in graph] # 存入度为0的顶点集合
for item in zero_in_degree:
for key, val in graph.items():
if item in val: # 图中含有该节点准备删除
val.remove(item) # 移除该顶点
if len(val) == 0: # 该顶点入度为0,则将该节点插入到0 degree 集合 下次继续遍历
zero_in_degree.append(key)
ordered.append(item)
return len(ordered) == numCourses
可以AC但是很慢,改良一下不用字典来存储
class Solution:
def canFinish(self, n, prerequisites):
G = [[] for i in range(n)] #表示图
degree = [0] * n
for j, i in prerequisites:
G[i].append(j)
degree[j] += 1
bfs = [i for i in range(n) if degree[i] == 0]
for i in bfs:
for j in G[i]:
degree[j] -= 1
if degree[j] == 0:
bfs.append(j)
return len(bfs) == n
这里他是从后往前删除的,degree[j] += 1 表示没有指出的顶点,先移除,然后再改变图中节点。比较巧妙的是只用了数组来存储,可能不是很直观,但是省去了字典删除操作,很高效。
另外就是用DFS,借助一个visit数组来保存当下访问节点的状态,初始化为0,正在访问为-1,访问结束为1表明安全无环,一旦深度遍历的过程中遇到visit值为-1,就表明图中有环存在,终止跑出False。代码如下:
def canFinish(self, numCourses, prerequisites):
graph = [[] for _ in xrange(numCourses)]
visit = [0 for _ in xrange(numCourses)]
for x, y in prerequisites:
graph[x].append(y)
def dfs(i):
if visit[i] == -1:
return False
if visit[i] == 1:
return True
visit[i] = -1
for j in graph[i]:
if not dfs(j):
return False
visit[i] = 1
return True
for i in range(numCourses):
if not dfs(i):
return False
return True
因为有一定的剪枝存在,所以效率相较于BFS会高一些。以上。
Leetcode-309 Best Time to Buy and Sell Stock with Cooldown 股票买卖
Say you have an array for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]
买股票题是一道经典的01背包变种问题,这些题有些可以变到你完全懵逼,我这里参考了花花酱算法的思路,是我看下来讲的最清楚的一个,我自己感觉是不太容易想到。
先来把概念分析做好,首先这里牵涉到3个动作:buy(买),sell(卖),rest(什么都不做)。然后对应的状态是:hold(买入持有状态),sold(卖出状态),rest(空仓状态)。在这个问题中,我们关心的是手上的资产,因此状态转移方程应该围绕hold,sold和rest3个状态来展开,01背包只有一个状态转移关系,可见这个问题还是比较复杂的。
根据题意,结合FSM(状态机)的概念,可以把对应的3个转移方程写出来:
- hold[i] = max(hold[i-1], reset[i-1] - price[i])
持有状态的价值 = max(前一时刻持有的价值,当前时刻买入的价值),由于买入之前一定要有cooldown,所以会产生第二种状态转变,注意买入的话是花钱,所以是减去当前股价。 - sold[i] = hold[i-1] + price[i]
卖出状态的价值 = 前一时刻的持有和当前卖出加钱的和,这里hold[i-1]因为是买入花钱,就一定是负数,所以是求和。 - rest[i] = max(rest[i-1], sold[i-1])
空仓状态的价值 = max(前一时刻空仓价值,卖出之后的价值)。因为卖出后必须要cooldown,所以这里的sold[i-1]也可以理解了。
上述三个状态的图得到如下:
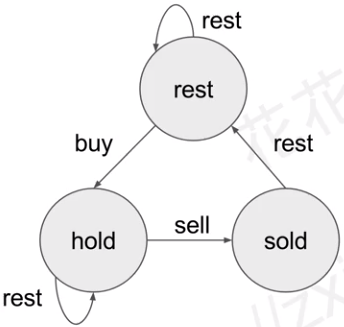
在初始值这里,hold[0] = -inf, sold[0] = 0, rest[0] = 0,这里hold的初始值不可以为0,因为买入是花钱持有的一定是负资产。
最终状态里,由于我们最后一个时刻不能买入股票,所以最优的状态一定是出现在rest和sold中,即要不最后一天正好卖出,要不最后一天依旧空仓。
然后我就可以非常顺畅的写下来代码了,一遍过,可见思想是何其重要,借助一个状态机解决了这么大的问题。
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
hold = [float('-inf')] * (len(prices) + 1)
sold = [0] * (len(prices) + 1)
rest = [0] * (len(prices) + 1)
prices.insert(0, None)
for i in range(1, len(prices)):
hold[i] = max(hold[i-1], rest[i-1] - prices[i])
sold[i] = hold[i-1] + prices[i]
rest[i] = max(rest[i-1], sold[i-1])
return max(sold[-1], rest[-1])
好像也可以写递归,也是差不多的意思了,有了状态转移方程什么都好办了,这里就不赘述了。
Leetcode-64 Minimum Path Sum 最小路径和
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example:
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
经典的DP题,脑子里立马会想到采用递归或者动态规划,递归自定向下,动态规划自下而上。
递归的思维就应该是递归用最终状态往前推,直到初始条件后输出结果。
动态规划的思维就是把大问题小规模化,借助2维数组来记录每一个小规模问题最优解,逐步递推到我们所求的解,说白了也就这么多东西。关键在于写出状态转移方程:
$$ route[i][j] = pos[i][j] + min(route[i-1][j], route[i][j-1])$$
解法一,递归+备忘录
class Solution(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
mem = {} # 备忘录
# route[i][j] = pos[i][j] + min(route[i-1][j], route[i][j-1])
def route(i, j):
if i < 0 or j < 0: # 超出边界时,我会主动返回一个正无穷给min()去做判断
return float('inf')
if i == 0 and j == 0:
return grid[i][j]
if (i, j) in mem:
return mem[(i, j)]
else:
mem[(i, j)] = grid[i][j] + min(route(i-1, j), route(i, j-1))
return mem[(i, j)]
if not len(grid) or not len(grid[0]):
return 0
return route(len(grid) - 1, len(grid[0]) - 1)
解法二,DP+二维数组
def minPathSum(self, grid):
m = len(grid)
n = len(grid[0])
# 补齐首行和首列
for i in range(1, n):
grid[0][i] += grid[0][i-1]
for i in range(1, m):
grid[i][0] += grid[i-1][0]
for i in range(1, m):
for j in range(1, n):
grid[i][j] += min(grid[i-1][j], grid[i][j-1])
return grid[-1][-1]
这是我摘取的一个大神的解法,写得贼清楚简洁,而且容易读懂,这才是写算法应该最终追求的。这边没有另外开辟存储空间,就直接在grid上做了输出,这里对第一行和第一列做了预处理,然后从(1,1)开始计算,最终输出右下角的结果。
这个题有时候还会不只是叫你输出最小值和,可能会让你列出最小值路径的详细情况,或者所有详细情况,这里可以拿到DP的解反推回去做一遍记录。另外也有其他变种的求法,比如从一点到另一点有几种走法,这个有点像爬楼梯问题,就不做过多介绍了。
Leetcode-763 Partition Labels 分割字符
A string S of lowercase letters is given. We want to partition this string into as many parts as possible so that each letter appears in at most one part, and return a list of integers representing the size of these parts.
Example 1:
Input: S = “ababcbacadefegdehijhklij”
Output: [9,7,8]
Explanation:
The partition is “ababcbaca”, “defegde”, “hijhklij”.
This is a partition so that each letter appears in at most one part.
A partition like “ababcbacadefegde”, “hijhklij” is incorrect, because it splits S into less parts.
这题有点懵逼的,一开始没什么思路,然后大致读懂了题意之后,脑子里又变得很乱,各种时间复杂度很高的算法都涌了出来,其实都没什么用。然后看到了这个题属于双指针和贪心,似乎给了我一点提示。借助一个字典来存储每个字母最后出现的索引,采用start和end双指针切割的思想,一旦end指针达到切割点便将数组切割,然后更新start节点以便下一次循环遍历得到。代码如下
import collections
class Solution(object):
def partitionLabels(self, S):
"""
:type S: str
:rtype: List[int]
"""
last_pos = {}
for idx, item in enumerate(list(S)):
last_pos[item] = idx
res = []
start, end = 0, 0
for index, item in enumerate(S):
if last_pos[item] > end:
end = last_pos[item]
# 到达切割点
if index == end:
res.append(end - start + 1)
start = end + 1
return res
这题复盘的时候,我在想怎么自己第一遍就不会想到这个思路呢,这题的关键无非就是了解题意之后。自己之前想用count来直接计数,然后发现边界条件很难写好,语句也不是很容易读,多了很多ifelse判断,但是用双指针以扩充范围的思想来看,就立马写的很顺了。
Leetcode-232 Implement Queue using Stacks 用堆栈实现队列
Implement the following operations of a queue using stacks.
push(x) – Push element x to the back of queue.
pop() – Removes the element from in front of queue.
peek() – Get the front element.
empty() – Return whether the queue is empty.
Example:
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // returns 1
queue.pop(); // returns 1
queue.empty(); // returns false
这是一道用栈来实现队列的问题,作为两种比较基本的数据结构,栈的特性是后进先出(LIFO),队列的特性是先进先出(FIFO)。因此这道题要实现的操作中,主要就是要实现push和pop不同数据结构之间的操作转化。
这里区别最大的一点就是push操作,堆栈只能放在顶部,因此pop时会出错,于是我们需要将push的元素放到头部,这样就和队列的数据结构保持一致了。这里借助另一个数组来实现这个功能,参考图:
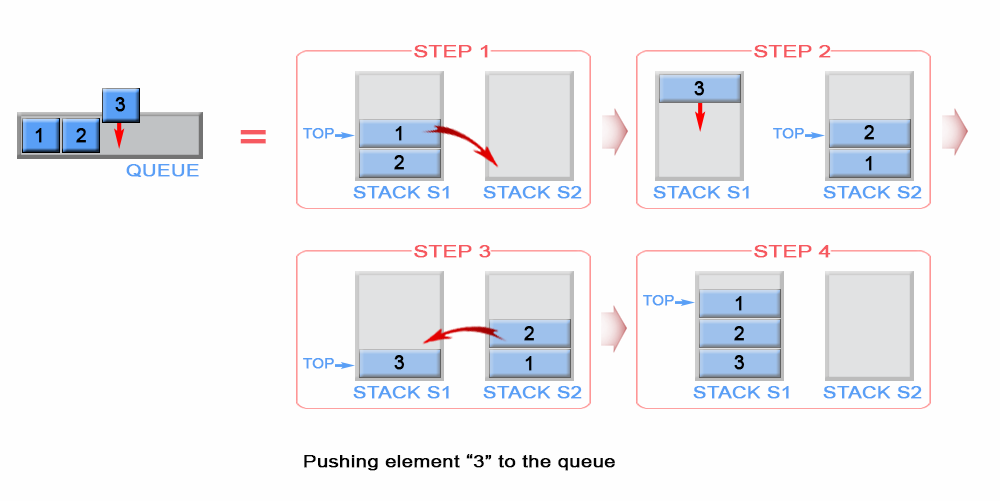
代码:
class MyQueue:
def __init__(self):
self.s1 = []
self.s2 = []
def push(self, x):
while self.s1:
self.s2.append(self.s1.pop())
self.s1.append(x)
while self.s2:
self.s1.append(self.s2.pop())
def pop(self):
return self.s1.pop()
def peek(self):
return self.s1[-1]
def empty(self):
return not self.s1
Leetcode-975 Odd Even Jump 奇偶跳
You are given an integer array A. From some starting index, you can make a series of jumps. The (1st, 3rd, 5th, …) jumps in the series are called odd numbered jumps, and the (2nd, 4th, 6th, …) jumps in the series are called even numbered jumps.
You may from index i jump forward to index j (with i < j) in the following way:
During odd numbered jumps (ie. jumps 1, 3, 5, …), you jump to the index j such that A[i] <= A[j] and A[j] is the smallest possible value. If there are multiple such indexes j, you can only jump to the smallest such index j.
During even numbered jumps (ie. jumps 2, 4, 6, …), you jump to the index j such that A[i] >= A[j] and A[j] is the largest possible value. If there are multiple such indexes j, you can only jump to the smallest such index j.
(It may be the case that for some index i, there are no legal jumps.)
A starting index is good if, starting from that index, you can reach the end of the array (index A.length - 1) by jumping some number of times (possibly 0 or more than once.)
Return the number of good starting indexes.
作死做了一道这么难的题,题目我都懒得摘下来了,太长了,有点 ACM的感觉。最近发现其实难题之所以难,一般是结合了2个以上的知识点,也可以说是一道题考察多个方面,代码层面也需要构建多个模块。我这里参考了花花酱的视频讲解 Link。
给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、4、6… 次跳跃称为偶数跳跃。
你可以按以下方式从索引 i 向后跳转到索引 j(其中 i < j):
在进行奇数跳跃时(如,第 1,3,5… 次跳跃),你将会跳到索引 j,使得 A[i] <= A[j],A[j] 是可能的最小值。如果存在多个这样的索引 j,你只能跳到满足要求的最小索引 j 上。
在进行偶数跳跃时(如,第 2,4,6… 次跳跃),你将会跳到索引 j,使得 A[i] => A[j],A[j] 是可能的最大值。如果存在多个这样的索引 j,你只能跳到满足要求的最小索引 j 上。
(对于某些索引 i,可能无法进行合乎要求的跳跃。)
如果从某一索引开始跳跃一定次数(可能是 0 次或多次),就可以到达数组的末尾(索引 A.length - 1),那么该索引就会被认为是好的起始索引。
输入:[2,3,1,1,4]
输出:3
解释:
从起始索引 i=0 出发,我们依次可以跳到 i = 1,i = 2,i = 3:
在我们的第一次跳跃(奇数)中,我们先跳到 i = 1,因为 A[1] 是(A[1],A[2],A[3],A[4])中大于或等于 A[0] 的最小值。
在我们的第二次跳跃(偶数)中,我们从 i = 1 跳到 i = 2,因为 A[2] 是(A[2],A[3],A[4])中小于或等于 A[1] 的最大值。A[3] 也是最大的值,但 2 是一个较小的索引,所以我们只能跳到 i = 2,而不能跳到 i = 3。
在我们的第三次跳跃(奇数)中,我们从 i = 2 跳到 i = 3,因为 A[3] 是(A[3],A[4])中大于或等于 A[2] 的最小值。
我们不能从 i = 3 跳到 i = 4,所以起始索引 i = 0 不是好的起始索引。
类似地,我们可以推断:
从起始索引 i = 1 出发, 我们跳到 i = 4,这样我们就到达数组末尾。
从起始索引 i = 2 出发, 我们跳到 i = 3,然后我们就不能再跳了。
从起始索引 i = 3 出发, 我们跳到 i = 4,这样我们就到达数组末尾。
从起始索引 i = 4 出发,我们已经到达数组末尾。
总之,我们可以从 3 个不同的起始索引(i = 1, i = 3, i = 4)出发,通过一定数量的跳跃到达数组末尾。
这道题,第一步重在列出递推公式。我们从后向前遍历:
如果第i个节点可以上升跳到队尾,那么只要前序的节点j能下降跳到i节点就算是成功True。
如果第i个节点可以下降跳到队尾,那么只要前序的节点j能上升跳到i节点就算是成功True。
所以递推公式可以得到一个间隔的形式:
odd[i] = even[j]
even[i] = odd[j]
因为要反应出递推的关系,所以我们加上另一个替代j的关系式:
odd[i] = even[odd_next[i]]
even[i] = odd[even_next[i]]
这里的odd_next和even_next反应那个odd和even的跳跃寻找符合条件的关系。其实能想到现在这一步,不算太难,但是在寻找奇偶分别条件上卡了很久,我只能想到一般的扫描,写的也不是很好看,说到底还是不熟。最后参考了大神的写法,发现小技巧其实很多,从倒序用reserved,到负数排序满足降序,再到用stack的退栈。最后,由于我们只能算odd的总和,因为每一个数都是从第一步开始跳算起的。
贴一下代码:
class Solution:
def oddEvenJumps(self, A):
"""
:type A: List[int]
:rtype: int
"""
odd = [False] * len(A)
even = [False] * len(A)
# 最后一个元素一定是满足的
odd[-1], even[-1] = True, True
oddNext = [None] * len(A)
evenNext = [None] * len(A)
# 用一个stack来存储最优值(最大或者最小)
# 返回出对应原数组的index, stack也是装的index
stack = []
for item, index in sorted([[item, index] for index, item in enumerate(A)]):
while stack and index > stack[-1]:
oddNext[stack.pop()] = index
stack.append(index)
stack = []
for item, index in sorted([[-item, index] for index, item in enumerate(A)]):
while stack and index > stack[-1]:
evenNext[stack.pop()] = index
stack.append(index)
for i in reversed(range(len(A) - 1)):
if oddNext[i] is not None:
odd[i] = even[oddNext[i]]
if evenNext[i] is not None:
even[i] = odd[evenNext[i]]
return sum(odd)
Leetcode-486 Predict the Winner 预测胜者
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
Example 1:
Input: [1, 5, 2]
Output: False
Explanation: Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return False.
Example 2:
Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
1 5 233 8
这道题,刚看有点没有太get到题意,这道题是一道有点博弈论背景的minmax的题,我也是看了花花酱的讲解有了一点认识。这里不能直接去拿最优的解,而是要转化成player1和player2的差来解决,因为题目只要求出player1可否胜利,因此,如果存在player1 - player2的差值大于0的话,就代表player1能成功。这里有一个坑,就是两个队员都要去尽量拿最优的结果,而不是只是那存在的结果,换句话说就是不能作弊。我刚开始看这道题的时候,也在想比如[1, 5, 2]中player1拿2,player2拿1,player1再拿5,这样player1也能赢。但是题设里有提到每个人都要尽量使得分数最大化。
既然两个选手都是比较聪明的,那我们也聪明一点。在这里的问题中,如果数字的个数是偶数个的化,player1一定可以赢,因为数字是可见的,player1有先手的优势,因此他完全可以找到预先找到最大的值安排顺序,换句话说就是他可以预知结果,比如[1, 5, 233, 7],player1可以知道233是最大值,因此他可以预先让自己能最终拿到这个数字,那么他为了保证一定能拿到233,那么他第一次就一定要拿1,这样player2只能从5和7中选择,如此就可以顺利成为赢家,其他偶数数字更大的情况也是一样适用的。而奇数就会存在不确定性,这个不确定性和player1多拿的数字有关。同之前的例子,如果这里数字变成了5个,那么也就是说player1会多取一个数字,剩下4个数字先手是player2,所以player2在偶数个的情况下是绝对可以保证自己赢的,那么player1到底能否最终成为赢家取决于,player1多取一个数字能否赢过偶数个情况下player2最优的情况。
这里的递推公式,可以写成
$$ solve(nums) = max(nums[0] - solve(nums[1:]), nums[-1] - solve(nums[:-1])) $$
解释一下,solve(nums)是每次最优的情况,而nums[0]和nums[-1]代表前一次取值的可能,而player1要赢,那么最后的solve的结果一定要大于等于0,才能赢。采用记忆化递归的方式,代码如下:
class Solution(object):
def PredictTheWinner(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if len(nums)%2 == 0 or len(nums) == 1:
return True
cache = dict()
def solve(nums):
tnums = tuple(nums)
if tnums in cache:
return cache[tnums]
cache[tnums] = max(
nums[0] - solve(nums[1:]),
nums[-1] - solve(nums[:-1])
)
return cache[tnums]
return solve(nums) >= 0
这么看代码不难,但是这个思路很难获得,也有用bottom-up做的,我没太看懂。。。感觉也有点复杂,列表格数组,就是不太容易想,直观是挺直观的。有时间再研究。
Leetcode-551 Student Attendance Record I 学生出席率
You are given a string representing an attendance record for a student. The record only contains the following three characters:
‘A’ : Absent.
‘L’ : Late.
‘P’ : Present.
A student could be rewarded if his attendance record doesn’t contain more than one ‘A’ (absent) or more than two continuous ‘L’ (late).
You need to return whether the student could be rewarded according to his attendance record.
Example 1:
Input: “PPALLP”
Output: True
Example 2:
Input: “PPALLL”
Output: False
感觉是道送分题,随便写了一下就AC了,这里需要注意的是缺席全局不能超过1次,迟到不能连续大于2次,直接就上代码了,思路也都是比较平铺直叙的。
class Solution(object):
def checkRecord(self, s):
"""
:type s: str
:rtype: bool
"""
count_a = 0
count_l = 0
max_l = 0
for item in list(s):
if item == 'A':
count_a += 1
count_l = 0
elif item == 'L':
count_l += 1
if count_l > max_l: max_l = count_l
else:
count_l = 0
return count_a < 2 and count_l < 3
这里可以稍微剪枝改进一下,在循环里一旦遇到缺席大于1次或者迟到连续达到3次的就直接输出False,否则则为True,代码如下:
class Solution(object):
def checkRecord(self, s):
"""
:type s: str
:rtype: bool
"""
count_a = 0
count_l = 0
for item in list(s):
if item == 'A':
count_a += 1
if item == 'L':
count_l += 1
else: count_l = 0
if count_a > 1 or count_l > 2:
return False
return True
Leetcode-1 2SUM 2数求和
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
Example:
Given nums = [2, 7, 11, 15], target = 9,
Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].
哈哈哈,又做回了第一题,是想借这个机会把所有的k-sum类题目都过一遍,先从这个2sum开始。作为第一题实在是有点简单,因为这里要返回原数组的索引,所以用一个dict来保存数据,key为数字,value为索引,代码如下:
class Solution:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
mem = dict()
for index, item in enumerate(nums):
if item in mem:
return [mem[item], index]
else:
mem[target - item] = index
这里是一个基本款,但是有一个适用于这里sum问题所有的情况的就是双指针,这里也不例外,虽然是有点麻烦,但是还是很有必要写一下的。
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
sn = sorted((num, i) for i, num in enumerate(nums))
i, j = 0, len(nums) - 1
print(sn)
while i < j:
n, k = sn[i]
m, l = sn[j]
if n + m < target:
i += 1
elif n + m > target:
j -= 1
else:
return [k, l]
这里将原数组,转化为(value, index)一个tuple类型。对这个tuple类型进行了排序,这样既保留了原有的index和value,又排了顺序。然后就是常规的步骤了,两个指针各指向一头,如果大于target就移动右指针,反之移动左指针。最近发现很多问题都有涉及对这个tuple的运用,真的是一个很高阶的技能。
Leetcode-15 3SUM 3数求和
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note: The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
和2Sum不同,这里是返回满足条件且不重复的结果,存储在一个list of lists里,既然是3Sum问题就会涉及到3个指针 ε==(づ′▽`)づ,看来是几sum就几个指针啊。这里比较棘手的是处理这个重复的问题,这里一度让我很头大,不过看了一些大神的方法,大家似乎也都是差不多的解决方案,那麻烦就麻烦点吧,代码如下:
class Solution:
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
nums.sort()
# 外层第1个指针
for i in range(len(nums)-2):
if i > 0 and nums[i] == nums[i-1]:
continue
# 第2第3个指针从i往后开始
l, r = i+1, len(nums)-1
while l < r:
s = nums[i] + nums[l] + nums[r]
if s < 0:
l +=1
elif s > 0:
r -= 1
else:
res.append((nums[i], nums[l], nums[r]))
# 这里判断直到找到下一个不同于上一个的值
while l < r and nums[l] == nums[l+1]:
l += 1
while l < r and nums[r] == nums[r-1]:
r -= 1
l += 1; r -= 1 # 这里把最终移动放到最后
return res
这里3个指针都需要去重,外层的i,去重判断为nums[i] == nums[i-1],内部的i和j,当满足条件时,插入结果,立马开始去重,直到找到下一个不重复的位置再继续带入while循环,直到 l==r 停止循环。
Leetcode-18 4SUM 4数求和
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.
Note: The solution set must not contain duplicate quadruplets.
Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
4数求和啦,一路从2个做到4个,这里也是一样的意思,4数就是4个指针喽(噗~(o゚▽゚)o)。一样也是会遇到很恶心的重复问题,我这里先自己丑陋的实现了一遍,思路是外层2个指针,内部做2SUM,去重我借助了一个字典,因为重复的情况很多很复杂,所以借助字典可以照顾到所有的情况,内外一旦发现重复,就启动指针的移位,最后输出结果中的每一个都先排了个序,再set去重,再转成list输出,哈哈哈,发现居然AC了。代码如下:
class Solution:
def writeDict(self, mem, key, value):
print(value)
if key in mem:
mem[key].append(value)
else:
mem[key] = [value]
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
mem = dict()
nums.sort()
res = []
for prior1_idx in range(len(nums)-2):
for prior2_idx in range(prior1_idx + 1, len(nums)-1):
sum_prior = nums[prior1_idx] + nums[prior2_idx]
prior = (nums[prior1_idx], nums[prior2_idx])
if sum_prior in mem and prior in mem[sum_prior]:
continue
sum_post = target - sum_prior
temp = nums.copy()
temp.remove(nums[prior1_idx])
temp.remove(nums[prior2_idx])
l, r = 0, len(temp) - 1
while l < r:
if temp[l] + temp[r] < sum_post:
l += 1
elif temp[l] + temp[r] > sum_post:
r -= 1
else:
post = (temp[l], temp[r])
if sum_post in mem and post in mem[sum_prior]:
l += 1
r -= 1
continue
else:
# 写入字典
self.writeDict(mem, sum_prior, prior)
self.writeDict(mem, sum_post, post)
single = list(prior) + list(post)
single.sort()
res.append(single)
l += 1
r -= 1
return list(set(tuple(i) for i in res))
很长,很不好用,但是能过,好了不耍流氓了。看了一些大牛的解法,终于是时候推出普适的解法了。
先贴一下代码:
class Solution:
# @return a list of lists of length 4, [[val1,val2,val3,val4]]
def fourSum(self, num, target):
num.sort()
def ksum(num, k, target):
i = 0
result = set()
if k == 2:
j = len(num) - 1
while i < j:
if num[i] + num[j] == target:
result.add((num[i], num[j]))
i += 1
elif num[i] + num[j] > target:
j -= 1
else:
i += 1
else:
while i < len(num) - k + 1:
newtarget = target - num[i]
subresult = ksum(num[i+1:], k - 1, newtarget)
if subresult:
result = result | set( (num[i],) + nr for nr in subresult)
i += 1
return result
return [list(t) for t in ksum(num, 4, target)]
这是我看下来写得比较清楚的一种,运用了递归,最小子问题就是一个普通的2sum双指针解法,在else里面,将外层的指针直到的数与target作差作为下一个k-1 sum的子任务目标值,进行递归求解。
result = result | set( (num[i],) + nr for nr in subresult)
这一行代码是关键,(num[i],)是tuple特有的形式,将之后满足的解灌入这个tuple中,外层用一个set包裹来达到去重的目的,因为双指针是依赖于排过序的。最后用result|来对所有的set取并集得到一个set of tuples的结果。最终,再把结果转化为list of lists就结束了。
这个办法,我觉得可能可以记忆一下,尤其是递归的思想和对结果的转化,真的不是短时间可以想到的,这里的2个模板,一个是基本的2sum,一个是ksum的转化,可以做一下记忆。(๑´ㅂ`๑)
Leetcode-77 Combination 组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
组合题,在第二周的记录上,曾经做过一个permutation的题,这两个题一般对照来看的,唯一区别在于,permutation可以重复,combination不可以重复。当时用dfs和backtracking都做过一遍,combination也用两种来处理一下。
首先是DFS,相对来说简单明了。模板就是for(或者while)循环里套上递归,进入递归函数第一步先判断是否满足条件,满足就插入到结果中,不满足继续递归。注意这里递归要加1,因为这是combination,不加一就是permutation了,不信你可以试试。代码如下:
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res = []
def dfs(array, k, path):
if k == 0:
res.append(path)
return
else:
for i in range(len(array)):
dfs(array[i+1:], k-1, path + [array[i]])
dfs(range(1, n+1), k, [])
return res
回溯法,等于是先构建了一棵很大的树,可以认为是贪心遍历所有结构了。用path记录贪心走过的所有路程,一旦走到结束或者遍历不满足,则回退,这里我们使用数组pop来回退。这里有一个加速的剪枝技巧,就是我们另外还需要的个数已经大于数组中可以取到的个数,那就直接return。代码如下:
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
res = []
if k==0 or n<1:
return res
def backtracking(n, k, path, index):
if len(path) == k:
res.append(path[:])
return
if k-len(path) > n - index + 1:
return
for num in range(index, n+1):
if num not in path:
path += [num]
backtracking(n, k, path, num+1)
path.pop()
backtracking(n, k, [], 1)
return res
两种方式都不错,而且可以当做模板来解决一堆类似的问题。相比较而言,dfs更符合人的理解,回溯这个pop还是需要习惯一下,不过也因熟练程度而异。
Leetcode-39 组合之和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
分析题目,给定目标值和一个数组,对于最终取得的元素重复没有做限制。因此采用DFS剪枝是我觉得比较好的方式,逻辑上实现比较清楚。构建dfs函数,3个参数,传入的array数组,没进行一次运算之后剩余要达到的target,以及记录累计的结果存入path中。2个截止条件,如果gap为0了,加入到结果中;如果gap小于当前数组中最小的元素了,说明不可能满足了,直接return回退。
这里对原始数组进行排序,可以达到剪枝的目的(一旦当前数字已经大于gap了,就直接return,不用再比较余下的数字了)。
算比较清楚,代码如下:
class Solution:
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
res = []
candidates.sort()
# path记录遍历过的数字
def dfs(array, gap, path):
if gap == 0:
res.append(path)
return
if gap < min(array):
return
for index, item in enumerate(array):
dfs(array[index:], gap - item, path + [item])
dfs(candidates, target, [])
return res
Leetcode-40 Combination Sum III 组合之和2
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
和之前的题目类似,但是要解决一个题目条件里的重复问题,我先想了一个比较tricky的办法,就是用set of tuple来解决重复问题,其余和77题是一样的。代码如下:
class Solution:
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
candidates.sort()
res = []
def dfs(array, gap, path):
if gap == 0:
res.append(path)
return
if len(array) >0 and gap < array[0]:
return
for index, item in enumerate(array):
dfs(array[index+1:], gap - item, path + [item])
dfs(candidates, target, [])
return [list(tupl) for tupl in {tuple(item) for item in res }]
可以AC,但是很丑陋。
唯一的区别在于如何处理重复,这里的重复比较讲究,因为要避免[1, 1, 5]也被归入重复的组合中,所以如何区分内层重复和外层重复就比较重要。举个例子来看,比如[10,1,2,7,6,1,5],排好序是[1, 1, 2, 5, 6, 7, 10],这里采用dfs就好比张开了一棵树:
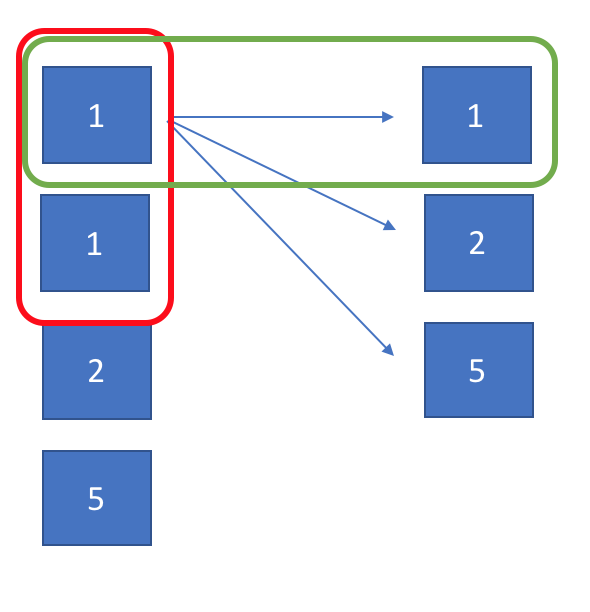
我们需要避免的是红色框,同级之间的重复,而对于跨层的重复是不需要处理的。因此index需要大于start,以保证我们是向后来检查同级是否有后续的数字有和当前重复的。这块其实不容易想,我花了好久时间才想明白,代码如下:
class Solution:
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
candidates.sort()
res = []
def dfs(array, start, target, path):
if target == 0:
res.append(path)
return
if target < 0:
return
for index in range(start, len(array)):
if index > start and array[index] == array[index-1]:
continue
dfs(array, index+1, target - array[index], path + [array[index]])
dfs(candidates, 0, target, [])
return res
Leetcode-216 Combination Sum III 组合之和3
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
这题基本和39题是一毛一样的,也没什么好讲的,两个条件,k的个数要等于0,且和等于target,同事满足即可,直接贴代码了。
class Solution(object):
def combinationSum3(self, k, n):
"""
:type k: int
:type n: int
:rtype: List[List[int]]
"""
nums = list(range(1, 10))
res = []
def dfs(array, target, path, k):
if target == 0 and k == 0:
res.append(path)
return
if target < 0 or k < 0:
return
for index in range(len(array)):
dfs(array[index+1:], target - array[index], path + [array[index]], k-1)
dfs(nums, n, [], k)
return res
Leetcode-328 奇偶链表
给定一个单链表,把所有的奇数节点和偶数节点分别排在一起。请注意,这里的奇数节点和偶数节点指的是节点编号的奇偶性,而不是节点的值的奇偶性。
请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1),时间复杂度应为 O(nodes),nodes 为节点总数。
示例 1:
输入: 1->2->3->4->5->NULL
输出: 1->3->5->2->4->NULL
示例 2:
输入: 2->1->3->5->6->4->7->NULL
输出: 2->3->6->7->1->5->4->NULL
我发现我一直不是很会做链表题,感觉可能少根筋,不过这道题还可以,题目意思是要将奇数位数字的node相连,将偶数位node相连,再拼接2个链表。
一般采取的方式是,dummy两个新的链表,将oddhead定义为奇数位头,evenhead定义为偶数位头,,再定义两个链表分别移动的指针为odd和even,因为是奇数和偶数位连接,所以要跳开一位,等2个链表内部串联好后,将odd的最后一个node连接上even链表,整个过程就完工啦,代码如下:
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def oddEvenList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head is None:
return None
odd=oddhead=head
even=evenhead=head.next
while even and even.next:
odd.next=odd.next.next
odd=odd.next
even.next=even.next.next
even=even.next
odd.next=evenhead
return oddhead
这里dummy两个新的链表,再分别用各自的头来遍历是链表题常用的技巧,链表的循环条件是next指针是null,因此也常用来练习while啦。
Leetcode-322 找零钱 coin change
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
一看要求最优解,就知道一定是一道动态规划的问题,这里在满足面值和的情况下,还要coin的数量最小,如果不满足的话,还要输出1。其实这个递推公式并不是特别的难写,我们当前的最优解,是由上一个的最优解加上1枚硬币得到的,因此就可以无限递推下去,列出递推公式如下:
$$
F ( S ) = \left{ \begin{array} { l l } { 0 , } & { \text { if } S = 0 } \ { \min _ { i = 0 , \cdots , n - 1 } F \left( S - c _ { i } \right) + 1 , } & { \text { if } S - c _ { i } \geq 0 } \ { - 1 } & { \text { other } } \end{array} \right.
$$
大致演算了一下:
dp[0] = 0
dp[1] = 1
dp[2] = min{dp[2-1]}+1
dp[3] = min{dp[3-1],dp[3-2]}+1
dp[4] = min{dp[4-1],dp[4-2]}+1
...
dp[11] = min{dp[11-1],dp[11-2],dp[11-5]}+1
这里需要额外注意的是,如果不存在的话,需要返回-1,因此在初始化的时候,将数组中的值全部化为正无穷inf,方便最后取不到的时候结果输出,当金额为0时即dp[0]=0,因为金额为0什么都不取。代码如下:
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
n = len(coins)
# dp[i]表示amount=i需要的最少coin数
dp = [float("inf")] * (amount+1)
dp[0] = 0
for i in range(amount+1):
for j in range(n):
# 只有当硬币面额不大于要求面额数时,才能取该硬币
if coins[j] <= i:
dp[i] = min(dp[i], dp[i-coins[j]]+1)
# 硬币数不会超过要求总面额数,如果超过,说明没有方案可凑到目标值
return dp[amount] if dp[amount] <= amount else -1
Leetcode-146 LRU缓存机制
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果关键字 (key) 存在于缓存中,则获取关键字的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字/值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作?
解题思想:这是一道常考的套路题,需要用到 2 种数据结构来解决问题,双向链表和哈希表;其中双向链表可以更好的定位到前后的元素,而哈希表是记录所有 key 所在的位置。LRU 的意义是最近最少使用,即如果一个页面是最近最少使用的,在到达 LRU 最大距离的时候就要弹出这个页面。具体分为 get 和 put 两个操作:
- get 操作:如果哈希表中有这个 key,则返回这个 key 的值,并且由于是最近使用的,所以需要将其移动至双向链表的头部;没有则返回-1
- put 操作:将(key,value)的一个 pair 加入到双向链表中,这边就存在 2 种情况:如果有则直接修改值,并且移动至链表头部;如果没有值,则新建链表节点,移动至头部,并且需要检查总的长度是否超过 LRU 总的容量,超过则要删除链表中最后一个节点,并且在哈希表里也要弹出这个节点对应的 key。
这块代码其实不难,但是需要自己新建双向链表,以及链表中删除移动等操作,核心考察的是数据结构的运用,贴一下代码:
class DLinkedNode:
def __init__(self, key=0, value=0):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
self.cache = {}
self.capacity = capacity
self.size = 0
self.head = DLinkedNode()
self.tail = DLinkedNode()
self.head.next = self.tail
self.tail.prev = self.head
def addToHead(self, node):
node.next = self.head.next
node.prev = self.head
self.head.next = node
node.next.prev = node
def removeNode(self, node):
print(node.key)
print(node.value)
print(node.next)
node.prev.next = node.next
node.next.prev = node.prev
def moveToHead(self, node):
self.removeNode(node)
self.addToHead(node)
def removeTail(self):
node = self.tail.prev
self.removeNode(node)
return node
def get(self, key: int) -> int:
if key not in self.cache:
return -1
# 如果 key 存在,先通过哈希表定位,再移到头部
node = self.cache[key]
self.moveToHead(node)
return node.value
def put(self, key: int, value: int) -> None:
if key in self.cache:
node = self.cache[key]
node.value = value
# move to the header
self.moveToHead(node)
else:
node = DLinkedNode(key, value)
self.cache[key] = node
# move to the header
self.addToHead(node)
self.size += 1
if self.size > self.capacity:
# remove the tail
removed = self.removeTail()
self.cache.pop(removed.key)
self.size -= 1